Als u een telescoop heeft aangekocht, zijn de verwachtingen ongetwijfeld heel hoog. Toch kan het zijn dat deze verwachtingen niet altijd voldoen aan het resultaat door de kwaliteit van de telescoop. In dit artikel wordt ondermeer besproken hoeveel een telescoop nu juist vergroot en welke afwijkingen deze kan hebben.
Hfdst 1.: Vergroten
Hoeveel vergroot deze telescoop? Dit is wellicht de meest voorkomende vraag die men stelt als men een telescoop ziet. Deze vraag is wel een goede vraag maar het antwoord daarop zegt helemaal niets over de kwaliteit van de telescoop. Er bestaan telescopen die 100x vergroten maar die relatief goedkoop zijn en er zijn er die maar 50x vergroten maar wel 10 keer zoveel kosten. De kwaliteit van de laatste is logischerwijze veel beter.
Hoe weet je nu hoeveel je telescoop vergroot?
De vergroting van je telescoop kan je heel gemakkelijk berekenen door de brandpuntsafstand van het objectief (fob) te delen door de brandpuntsafstand van het oculair (foc). Dit vormt dus: fob: foc
Voorbeeld: De brandpuntsafstand van het objectief is 1 meter en dat van je oculair is 1 centimeter dan is de vergroting (V= 100:1) gelijk aan 100x.
Als we nu een oculair nemen met een brandpuntsafstand van een halve centimeter zal de vergroting gelijk zijn aan 200x.
De minimale vergroting (Vmin)
Als we een groot gezichtsveld willen hebben met onze telescoop en tegelijkertijd een zeer helder beeld willen hebben (wordt het meest toegepast voor het zoeken en waarnemen van kometen, nevels, galaxieën ...) kiezen we best voor een zo klein mogelijke vergroting. Maar om het gehele telescoopobjectief te benutten, moeten we ervoor zorgen dat alle stralen die in de telescoopbuis terechtkomen ook allemaal in het oog komen.
Nu gaan alle stralen die in het objectief vallen ook door de uittreepupil van de telescoop. Als we dus zorgen dat de uittreepupil niet groter is dan de oogpupil, gaat er geen licht verloren.
Bij nachtelijke waarnemingen is de middellijn van onze oogpupil ongeveer 8mm. De uittreepupil van de telescoop mag dus maximaal 8mm zijn, zodat de minimale vergroting gelijk is aan:
Vmin = D : 8 = 1/8 D (D= middellijn van het objectief in mm)
Voorbeeld: Bij een 10cm objectief is dus de minimale vergroting: Vmin = 100 : 8 = 12,5x
De optimale vergroting (Vopt)
Bij een bepaalde vergroting worden zowat alle details zichtbaar die, in het beeld dat het objectief vormt, aanwezig zijn. Als je dan verder vergroot, geeft dit niet meer details, ze komen enkel wat verder uit elkaar te liggen maar het beeld lijkt niet helemaal scherp te zijn. Deze vergroting noemt men dan de optimale of de beste vergroting van uw telescoop. De optimale vergroting ligt tussen de D en een halve D, afhankelijk van de gezichtsscherpte van ons oog. Hierdoor krijgen we de volgende formule:
Vopt = 1/2 D à D
Voorbeeld: De optimale vergroting bij een objectief van 80mm is dus 40 à 60x
Voor de meeste astronomische waarnemingen zullen we dus de optimale vergroting kiezen.
De maximale vergroting (Vmax)
Voor het waarnemen van dubbelsterren en voor het testen van objectieven heeft het wel eens nut om boven de optimale vergroting te gaan.
Het geeft geen zin dat je boven de maximale vergroting gaat!
Nadelen van een te grote vergroting
- Een klein gezichtsveld.
- De hemellichamen verdwijnen snel uit het beeldveld en we moeten de kijker voortdurend bijstellen.
- De helderheid is te klein, behalve bij de sterren.
- Atmosferische storingen beïnvloeden het beeld sterker.
- Last van onvolmaaktheden van de montering (trillingen) en een eventueel volgmechanisme.
- De geringste fouten van het objectief worden ook hinderlijker.
Je kan de maximale vergroting eenvoudig zelf berekenen door deze formule:
Vmax = 2 D
Voorbeeld: Een telescoop met een diameter van 75mm levert een maximum vergroting op van 150x
De maximum vergroting is enkel geldig voor kleinere objectieven tot 15cm en een zeer rustige atmosfeer. Het is daarmee ook raadzaam om geen oculair te kopen dat de maximale vergroting overschrijdt.
Licht verzamelen
De "grootte" van de telescoop wordt gekenmerkt door de middellijn van het objectief op te geven. Zo spreken we van een 75mm telescoop of een 10 cm telescoop.
Van deze middellijn (D) is afhankelijk hoeveel licht er tenslotte door onze pupil naar binnen komt , want door de optiek van de kijker wordt een lichtbundel met de middellijn D vernauwd tot een bundel met een middellijn die kleiner is of gelijk aan de oogpupil.
Voorbeeld: Als we een kijker hebben met een objectiefmiddellijn van 5cm en nog een telescoop met een objectiefmiddellijn van 10cm, dan vangt de 2de telescoop 4 maal zoveel licht als de eerste telescoop.
De lichtsterkte van de kijker is dus evenredig met het kwadraat van de objectiefmiddellijn.Hierdoor krijgen we volgende formule:
Lichtsterkte = 0,6 D2 :d2
D= de middellijn van het objectief
d= de middelijn van de oogpupil
factor 0,6= lichtverlies door terugkaatsing en absorptie in de optiek van de telescoop
Hoe groter de lichtsterkte van de kijker, hoe zwakker ook de sterren, die nog net nog te zien zijn met de telescoop.
In onderstaande tabel staat aangegeven welke magnituden van sterren nog net te zien zijn:
| D (in cm) | Magnitude (m) |
|---|---|
| 2.5 | 10 |
| 5 | 12 |
| 7,5 | 13 |
| 10 | 13,5 |
| 12,5 | 14 |
| 15 | 14,5 |
| 20 | 14,8 |
| 25 | 15,2 |
| 30 | 15,6 |
| 40 | 16 |
| 250 | 18,8 |
De helderheid van een object is afhankelijk van de vergroting. Nemen we de vergroting 2 maal zo groot, dan wordt de helderheid 4 maal zo klein; de helderheid is omgekeerd evenredig met het kwadraat van de vergroting.
De nachtelijke hemelachtergrond zelf is nooit helemaal donker; deze gedraagt zich dus als een zeer lichtzwak uitgebreid hemellichaam.
Daaruit volgt, dat bij sterkere vergrotingen de achtergrond donkerder wordt ten opzichte van de sterren.
Gaat het er dus om een zeer lichtzwak sterretje, op de grens van wat de kijker kan presteren, nog te zien, dan moeten we een sterke vergroting gebruiken. De helderheid van de ster is onafhankelijk van de vergroting, maar bij sterkere vergrotingen wordt wel de achtergrondhelderheid kleiner, zodat het contrast groter wordt.
Hfdst 2.: Gestoken scherp en de spelbreker
Het buigingsschijfje
Als het objectief van onze kijker geen afbeeldingsfout heeft, zouden we kunnen verwachten dat alle lichtstralen die van 1 punt (zoals een ster) uitgaan weer in één punt in het brandvlak samenkomen.
Dit is niet zo. Het ligt in wezen dat in het brandvlak een cirkelvormig lichtvlekje ontstaat (het buigingsschijfje van Airy).
Dit vlekje bestaat uit een helder centrum, omgeven door minder heldere lichtcirkels.
Bij instrumenten waar de stralengang van het objectief naar het oog niet onderbroken is (zoals een lenzenkijker), komt circa 80% van al het licht in het centrale schijfje (dat we op een scherm of fotografische plaat in het brandvlak kunnen opvangen) is te berekenen uit:
d= (7 / 10.000) x (fob / D) mm
D= middellijn van het schijfje
fob= brandpuntsafstand van het objectief
7/10.000 = een afgerond getal waarin ook de golflengte van het licht verrekend is.
Voorbeeld:
Een kijker met een objectief met een middellijn van 5cm en een brandpuntsafstand van 60cm geeft dus een buigingsschijfje met een middelijn van:
d= (7 / 10.000) x (60 / 5) = 0,0084 mm
Als met de kijker foto's worden gemaakt, is het van belang de middellijn van het buigingsschijfje te kennen. Maar bij visuele waarnemingen kunnen we de "scherpte" (het zogenaamde scheidend vermogen) anders uitdrukken.
Als 2 sterren dicht bij elkaar staan, zullen we met een kijker met een groot scheidend vermogen 2 puntjes kunnen zien, terwijl er met een kijker met een klein scheidend vermogen slechts één klein puntje te zien is. Het scheidend vermogen drukken we dan uit in de hoekafstand (in boogseconden) die de sterren mogen hebben om ze nog juist als twéé sterren te kunnen onderscheiden.
Dit scheidend vermogen (aangeduid door letter s) hangt af van de middellijn (D) van het objectief.
s = 120° / D (D in mm)
Een kijker met een objectief van 5cm middellijn zal dus nog dubbelsterren kunnen onderscheiden die 2,4 boogseconden van elkaar staan, want s = 120° / 50 = 2,5"
Als we een dubbelster hebben waarvan de 2 sterren 1 boogeseconde van elkaar zijn verwijderd, zullen we met een 5cm kijker nooit de 2 sterren zien, al nemen we een sterkere vergroting .
Met behulp van de formule kunnen we dus volgend lijstje samenstellen:
| Middellijn objectief (ongewapend oog) | Scheidend vermogen (4' = 240") |
|---|---|
| 1 cm | 12" |
| 2 cm | 6" |
| 4 cm | 3" |
| 5 cm | 2.4" |
| 6 cm | 2" |
| 8 cm | 1.5" |
| 10 cm | 1.2" |
| 15 cm | 0.8" |
| 20 cm | 0.6" |
| 25 cm | 0.48" |
| 30 cm | 0.4" |
Nu moet je niet denken dat een kijker met een perfect geslepen spiegel of lenzenstelsel dit theoretisch scheidend vermogen ook haalt. Kleinere lenzenkijkers halen het eenvoudig maar grotere niet.
Maximale vergroting
Ons oog ziet twee lichtpunten pas afzonderlijk als ze een hoek van ongeveer 4' met elkaar maken (4 minuten = 4 x 60" = 240").
Bij een 5cm objectief (zie lijst van scheidend vermogen hierboven) is een vergroting van 240 / 2,4 = 100 X nodig. Dit is dus ook de bovenste grens der vergroting die nog enig nuttig effect heeft bij het waarnemen van dubbelsterren . Deze grens noemen we Vmax. Ze bedraagt tweemaal de middellijn van het objectief in milimeter.
In het algemeen is het oplossend vermogen 120" / D
Bij een vergroting V wordt deze hoek: 120" / D x V
Als de hoek 4' of 240" is, zitten we aan de grens der vergroting omdat dan de buigingsschijfjes zichtbaar worden en niet meer puntvormig lijken. Dus voor de maximum vergroting geldt:
120" / D x V = 240"
Hieruit volgt Vmax = 2D
We zullen zien dat we deze vergroting alleen in bijzonder goede omstandigheden kunnen gebruiken.
Bepaling van het scheidend vermogen met een testkaart
Het scheidend vermogen van je telescoop bepalen is heel moeilijk door op te geven wat je er allemaal mee ziet. Hiervoor hebben we een meer onpersoonlijke meetmethode voor. Om je telescoop te testen zouden we best nagaan hoeveel dubbelsterren we nog net gescheiden kunnen zien. Van een groot aantal dubbelsterren is namelijk de boogafstand aan de hemel bekend. Dit is een onmogelijk en enorm tijdrovend werk waarbij het weer meestal roet in het eten gooit.
We kunnen het scheidend vermogen met een testkaart berekenen:
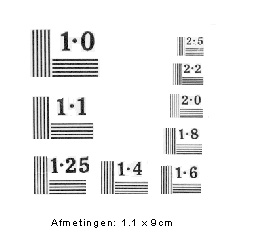
Hierop zien we groepjes met steeds dichterbijstaande zwarte en witte lijnen.
We stellen de testkaart zo op dat hij goed verlicht wordt en bekijken dan de kaart op een afstand van 25 à 100 meter door onze kijker met ons sterkste oculair.
Voorbeeld:
We staan op een afstand van 52,5 meter, we bestuderen de testkaart en zoeken het groepje op, dat we nog net als witte en zwarte lijntjes zien. Nu nemen we aan dat dit het groepje is waar 1,25 staat, dan zien we het groepje 1,4 in het grijs. We moeten waarnemen in rustige ogenblikken en daarom houden we 1,4 nog even in de gaten telkens als de lucht rustig is. Blijft 1,4 grijs, dan blijven we bij 1,25.
Met de volgende formule vinden we dan het scheidend vermogen in boogseconden:
S = 206 / (A . N)
A= Afstand in meter
N = goede groepnummer
In ons geval is het scheidend vermogen dus:
S = 206 / (51,5 . 1,25) = 3,2"
Om te beoordelen hoe goed onze kijker is, vergelijken we de uitkomst met het theoretisch scheidend vermogen van onze kijker. We gaan de kwaliteit ook uitdrukken in procent. Hiervoor gebruiken we volgende formule:
K = 100 maal het theoretisch scheidend vermogen
Werkelijk scheidend vermogen
Stel dat de telescoop een objectiefmiddellijn van 5cm heeft (het theoretisch scheidend vermogen is dus 2,4"), dan is de kwaliteit:
K = (240 / 3,2) = 75%
Met het kleine testkaartje kunt u alle telescopen testen. Is 2,8 nog helemaal te zien, vergroot dan uw afstand. Is 1,0 nog volledig te zien, dan verkleint u de afstand.
Spelbreker: de atmosfeer
Meestal komt het volledige scheidend vermogen niet bij onze waarnemingen tot zijn recht. Er is een spelbreker en dat is de atmosfeer.
De atmosfeer werkt als een zware filter die allerlei stralingen tegenhoudt. Een verontreinigde en onrustige atmosfeer is te vergelijken met een filter van zeer slecht glas waarin slierten en bobbels voorkomen. De grote telescopen worden daarom enkel op hoge bergen in een gebied met een gunstig klimaat geplaatst .
In ons land is het evenmin geschikt om astronomische waarnemingen te verrichten. Niet alleen omdat er weinig onbewolkte nachten zijn, maar omdat in die onbewolkte nachten de atmosfeer niet zo rustig is.
Voorbeeld: Een heldere vriesnacht met vele fonkelende sterren is zeer ongunstig
van een buigingsschijfje als beeld van een ster is dan geen sprake meer. Het beeld is groter dan het theoretisch te verwachten buigingsschijfje en danst het op en neer en kronkelt zich in allerlei vormen.
Hoe dichter de ster of planeet bij de horizon staat, des te slechter het beeld wordt omdat we nabij de horizon door een 10 maal zo dikke luchtlaag heen kijken als bij het zenith. Een stand van 40° boven de horizon is gunstig te noemen.
De meest gunstige nachten om te waarnemen, vallen in het najaar. Dan gebeurt het meestal dat er een lichte mist of nevel hangt terwijl de atmosfeer heel rustig is, dan kan je telescoop echt laten zien wat hij waard is. Bij sterke vergrotingen zien we het buigingsschijfje omgeven door lichte ringen.
We bekijken b.v. de maan bij een vergroting van V = D en het is bijna onmogelijk om scherp te stellen; plotseling echter wordt het vage beeld haarscherp om daarna weer te vervagen, zonder dat we de instelling veranderd hebben.
De geoefende waarnemer maakt juist van zulke ogenblikken van goede 'seeing' gebruik.
De telescopen met een kleine objectiefmiddellijn hebben minder last van de onrust van de atmosfeer dan die met grotere middellijn omdat de in een kleinere kijker vallende lichtbundel door een dunnere pijp van onrustige lucht is gegaan.
Bij zeer onrustige atmosfeer heeft zelfs een kijker met een kleinere objectiefdiameter een groter scheidend vermogen dan een kijker met grotere objectiefdiameter. Dit is de reden waarom het in ons klimaat weinig zin heeft telescopen te gebruiken met een grotere objectiefdiameter dan 20 cm. Het laatste stukje dat het licht in de atmosfeer moet afleggen, kan dikwijls het beeld totaal bederven. We bedoelen de lucht in de kijkerbuis tussen het objectief en het oculair. Als de telescoop uit een warmere omgeving (binnen) in een koudere (buiten) komt of omgekeerd, ontstaan er in de buis luchtstromingen. Het beeld wordt daardoor onscherp, het lijkt of het 'kookt'.
Er zijn twee effectieve middelen om dit tegen te gaan.
- Neem de telescoopbuis 2 cm groter in diameter dan het objectief en bekleed de binnenkant met een plaat kurk van +/- een 0,5 cm dikte.
- Zet het instrument direct na zonsondergang buiten, zodat het de temperatuur van de buitenlucht aanneemt (Dit moeten we in elk geval doen om het objectief de temperatuur van de omgeving te laten aannemen. Bij grotere spiegels (bv. 20 cm) kan dit wel 'n uur duren.).
Het eerste heeft alleen zin bij gesloten kijkertypen. Tot het tweede moeten we wel onze toevlucht nemen bij open kijkers. We moeten er ook rekening mee houden dat ons lichaam warmte afgeeft. Houden we b.v. de kijkerbuis met de hand vast, dan ontstaan ook luchtstromingen. Sommige plaatsen zijn zeer ongeschikt om een kijker te plaatsen, omdat de lucht er te onrustig is: b.v. in een stad stijgt in de winternachten een voortdurend trillende warme luchtkolom op. En 's zomers als overdag de 'stenen stad' goed verwarmd is geweest, krijgen we hetzelfde effect in de voornacht. De nanacht is dan de beste waarnemingstijd.
Voor wie wil weten, wat de beste plaats is voor het opstellen van zijn telescoop, geven we de volgende beschrijving, die echter voor ons land geen enkel praktisch nut heeft. Een droog plateau ca. 1000 m boven de zeespiegel, bedekt met plantengroei, in een droog klimaat met veel heldere nachten, ver verwijderd van de zee, van dalen en van steden.
Het oog, het laatste deel van het optisch stelsel
Dit zijn enkel details die bij astronomische waarnemingen van belang zijn.
Het oog kunnen we beschouwen als een positieve lens met een brandpuntsafstand van ongeveer 15mm waarachter de gevoelige laag: het netvlies zit.
Op 1 mm van het netvlies wordt ongeveer 4° afgebeeld. Er zijn twee soorten gevoelige elementen (of zenuwuiteinden) in het netvlies:
- De kegeltjes, die gevoelig zijn voor kleur en die alleen in het centrum van het netvlies voorkomen.
- De staafjes, die buitengewoon gevoelig zijn voor licht, ze zijn echter wel "kleurenblind".
Bij astronomische waarnemingen komen vooral deze staafjes in aanmerking. Omdat deze staafjes echter niet voorkomen in het centrum van het netvlies, zullen zwakkere sterren onzichtbaar zijn als we ze fixeren, om die te zien moeten we er net even naast kijken.
Als we van het licht in het donker komen (dus bij het begin van het waarnemen) gebeuren er verschillende dingen. De oogpupil verwijdt zich. Ze krijgt een viermaal zo grote middellijn en we ontvangen dus 16-maal zoveel licht. Maar gaat zich in het netvlies echter een stof (gezichtspurper) vormen, die de staafjes veel lichtgevoeliger maakt. Dit duurt ongeveer 20 minuten. Het oog is dan 100 000 maal zo gevoelig geworden! Vitamine-A-gebrek is oorzaak van het slecht vormen van gezichtspurper (nachtblindheid) en ok nicotine verhindert de snelle vorming van gezichtspurper.
Het waarnemen van de maan, planeten en heldere sterren gebeurt natuurlijk wel in het centrum van het gezichtsveld met de kegeltjes; daarom kunnen we makkelijk kleur onderscheiden.
Echt waarnemen vermoeit het oog snel. De kunst van het waarnemen bestaat erin om snel te zien wat men wil zien om daarna het oog weer wat rust te geven.
Hierbij kan ook opgemerkt worden dat het van belang is de kijker zodanig op te stellen dat men al zittend kan waarnemen. Elke onnatuurlijke houding maakt een langdurige waarneming tot een kwelling.
Elk normaal oog is wat astigmatisch, heeft sferische en chromatische aberratie. Bij sterke vergrotingen zijn de invallende bundels smal (denk hierbij aan de uittreepupil) en dan worden deze fouten opmerkelijk klein.
Men kan zelfs zeggen dat ze niet meer waarneembaar zijn als de uittreepupil kleiner is dan 2mm. Maar bij zulke smalle bundels treedt er een ander hinderlijk verschijnsel op. In het oogvocht zweven kleine verontreinigingen rond (vb.: dode cellen) en deze worden zichtbaar als kleine schijfjes en slierten. Bij het staren naar een egaal zwak verlicht vlak (zoals een onbewolkte hemel in de schemering) ziet men deze duidelijk.
Deze onregelmatigheden zijn hinderlijk bij het waarnemen als ze de nauwe invallende bundel passeren.
Een waarnemer die verziend of bijziend is, kan gerust zonder bril waarnemen, alleen zal hij de kijker iets moeten bijfocussen. Waarnemen zonder bril is prettiger omdat men dan van het gehele gezichtsveld gebruik kan maken. Als het oog sterk astigmatsch is, zodat men cilindrische glazen ter correctie daarvan draagt, kan men de bril echter niet missen.








